PyTorch自动求导、torch.no_grad()、优化器
日期:2024-04-15 11:58 | 人气:
【PyTorch深度学习实战】Chapter 5 代码、图片资料:https://box.lenovo.com/l/mu2L0y
本章主要讲解PyTorch自动求导机制、torch.no_grad()作用、优化器使用。
在本章开篇,作者借用了开普勒发现开普勒定律的过程:利用他的朋友Brahe的数据拟合模型,确定椭圆的模型,不断迭代拟合最优的离心率和大小,最终推出了开普勒三大定律,来说明学习就是参数估计,本章要讲的就是如何利用PyTorch对构建的模型进行参数拟合。
下图是本章的概括,其实也很好理解:给定输入数据和相应的期望输出,以及权重的初始值,给模型输入数据(正向传播),并通过对输入结果与实际数据进行比较来评估误差。为了优化模型参数,即它的权重,权重的变化是使用复合函数导数的链式求导法则计算的(反向传播)。然后,在使误差减小的方向上更新权重值,重复该过程,直到根据未知的数据评估的误差降到可接受的水平。
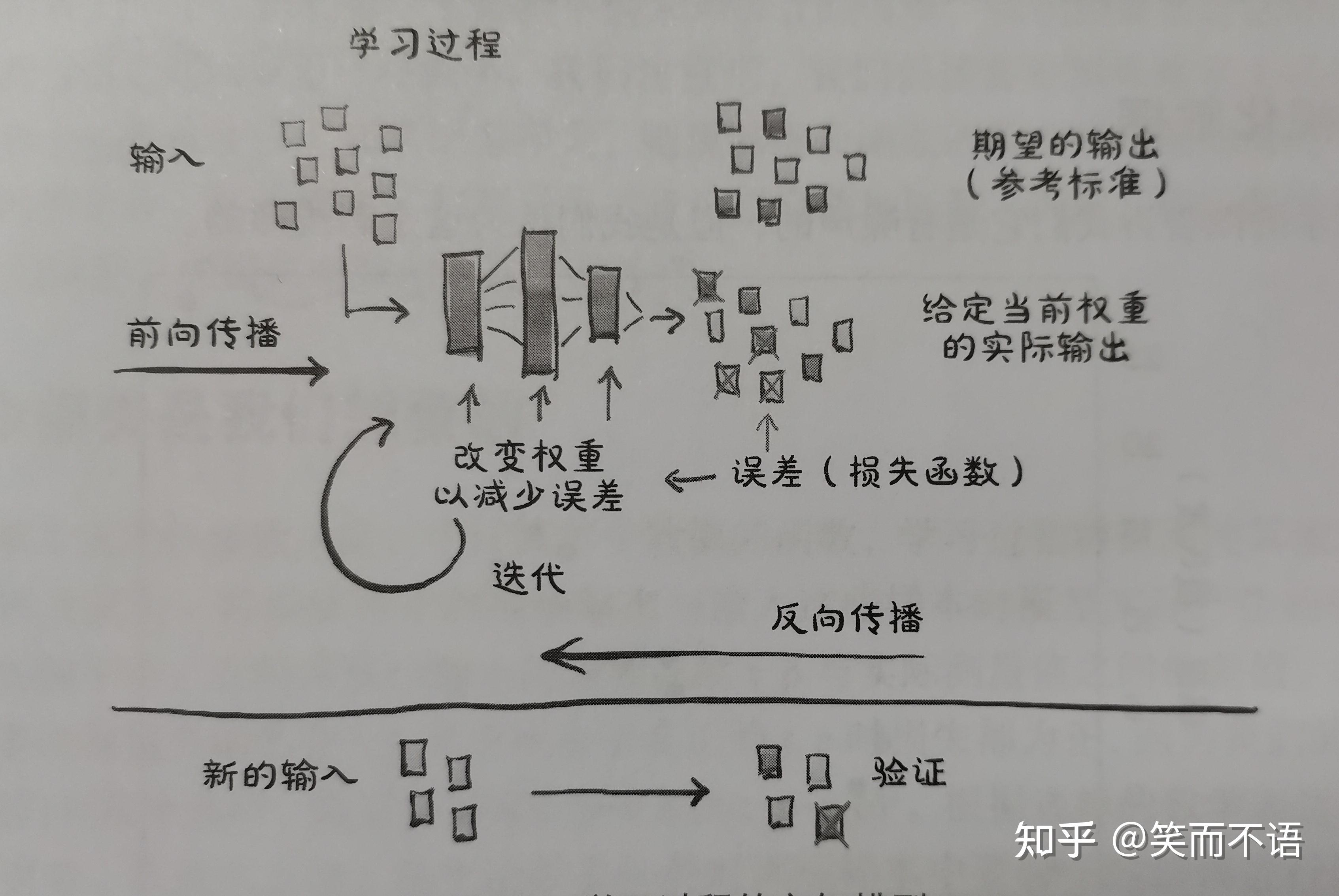
下面的介绍皆围绕一个例子:有一个不显示单位的温度计,我们期望基于已有带单位的温度计进行测量,接着记录下该温度计的数值,探寻他们之间的关系,进而确定新的单位是什么。
首先导入数据,t_c是已知的带单位(℃)的温度计显示,而t_u是我们未知单位温度计的数值,中间必然会存在一些噪声:
%matplotlib inline
import numpy as np
import torch
t_c = [0.5, 14.0, 15.0, 28.0, 11.0, 8.0, 3.0, -4.0, 6.0, 13.0, 21.0]
t_u = [35.7, 55.9, 58.2, 81.9, 56.3, 48.9, 33.9, 21.8, 48.4, 60.4, 68.4]
t_c = torch.tensor(t_c)
t_u = torch.tensor(t_u)可视化一下:
%matplotlib inline
from matplotlib import pyplot as plt
fig = plt.figure(dpi=150)
plt.xlabel("Measurement")
plt.ylabel("Temperature (°Celsius)")
plt.plot(t_u.numpy(), t_c.numpy(), 'o')
根据上图,我们的模型可能是一个线性的,即对t_u乘上一个系数w,加上一个常数b,我们就可以得到摄氏温度:
下面的优化目标就是拟合最优的w和b,使得损失函数处于最小值。从概念上讲,损失函数是一种对训练样本中要修正的错误进行优先处理的方法,因此参数更新会导致对高权重样本的输出进行调整,而不是对损失较小的其他样本的输出进行调整。
我们采用 作为我们的损失函数,
是模型的预测温度输出,并且由于该损失函数是凸函数,所以找到其极小值较为容易。值得注意的是,平方差比绝对误差对错误结果的惩罚更大,通常有更多轻微错误的结果比有少量严重错误的结果更好,而平方差优先处理高误差的输出,效果较好。
下面定义我们的模型和损失函数:
def model(t_u, w, b):
return w*t_u+b
def loss_fn(t_p, t_c):
squared_diffs = (t_p - t_c)**2
return squared_diffs.mean()现在初始化参数,并调用模型:
w = torch.ones(())
b = torch.zeros(())
t_p = model(t_u, w, b)
t_p
'''
tensor([35.7000, 55.9000, 58.2000, 81.9000, 56.3000, 48.9000, 33.9000, 21.8000,
48.4000, 60.4000, 68.4000])
'''
loss = loss_fn(t_p, t_c)
loss # tensor(1763.8848)下面的问题是,如何估计w和b,使损失达到最小?我们首先通过手动方式来解决问题,后面再去理解PyTorch的机制。
接下来,章节叙述了如果手动对二次的损失函数手动求导,计算梯度,并应用于模型更新中,接着,指出了学习率过大过小对模型收敛的影响,最后,注意到:第1个迭代周期,权重的梯度是偏置梯度的50倍,因此一个学习率对于这两个参数的收敛的效果是不一样的,因此我们需要归一化权重,偏置的输入,使得他们的范围近似相等,这样才能用一个学习率对两个变量都很好的训练。因为这部分主要是梯度下降的原理说明以及代码的简单演示,在此不再赘述。对于梯度下降,可以参见我觉得很好的一篇教程:人工神经网络背后的数学原理!。
下面直接介绍PyTorch的自动求导机制。
在第3章中,就已经介绍过张量,但有一个容易忽略的点:PyTorch张量可以记住它们从何而来,即可以根据产生它们的操作和其父张量,自动提供这些操作的导数链(grad_fn),这意味着我们不需要真的手动计算梯度,只要给定一个前向表达式,无论嵌套方式如何,PyTorch都可以自动提供表达式相对其输入参数的梯度。
回到我们的模型定义与损失函数:
def model(t_u, w, b):
return w*t_u+b
def loss_fn(t_p, t_c):
squared_diffs = (t_p - t_c)**2
return squared_diffs.mean()初始化一个参数张量:
params = torch.tensor([1.0, 0.0], requires_grad=True)注意到这个requires_grad参数,这个参数告诉PyTorch跟踪由对params张量进行操作后产生的张量的整个系谱树(计算图),换句话说,任何将params作为祖先的张量都可以访问从params到那个张量的函数链。如果这些函数是可微的(大多数操作函数都是可微的),导数的值将自动填充到params的grad属性中(这就是自动求导)。
试一下:
loss = loss_fn(model(t_u, *params), t_c)
loss.backward()
params.grad # tensor([4517.2969, 82.6000])通过backward()进行反向求导。此时,params的grad属性包含关于params的每个元素的损失函数的梯度值。要注意,调用backward()将导致梯度在在叶子节点上累加,也就是说,如果我们反复运行上述代码,params.grad的值是会越来越大的。因此,我们需要在每次反向传播,参数更新之后,显式的将梯度归零。
利用zero_()方法可以很轻易的做到:
if params.grad is not None:
params.grad.zero_()
params.grad # tensor([0., 0.])那么,为什么PyTorch不直接在backward()中设置,调用结束后梯度自动归0呢?不这样做的目的是为了在复杂模型中梯度的使用提供更多的灵活性和控制性。
综上,可以修改得到我们的自动求导训练的代码:
def training_loop(n_epochs, learning_rate, params, t_u, t_c):
for epoch in range(1, n_epochs + 1):
# 在backward()前即可
if params.grad is not None:
params.grad.zero_()
t_p = model(t_u, *params)
loss = loss_fn(t_p, t_c)
loss.backward()
with torch.no_grad():
params -= learning_rate * params.grad
if epoch % 500 == 0:
print('Epoch %d, Loss %f' % (epoch, float(loss)))
return params
training_loop(n_epochs = 5000, learning_rate = 1e-2, params = torch.tensor([1.0, 0.0], requires_grad = True), t_u = 0.1 * t_u, t_c = t_c)
'''
Epoch 500, Loss 7.860115
Epoch 1000, Loss 3.828538
Epoch 1500, Loss 3.092191
Epoch 2000, Loss 2.957698
Epoch 2500, Loss 2.933134
Epoch 3000, Loss 2.928648
Epoch 3500, Loss 2.927830
Epoch 4000, Loss 2.927679
Epoch 4500, Loss 2.927652
Epoch 5000, Loss 2.927647
tensor([ 5.3671, -17.3012], requires_grad=True)
'''params的更新并不像我们想的那么简单
1.在更新params时,代码块是放在了with torch.no_grad()当中的,这个上下文管理器的作用是阻止自动求导机制对params的继续跟踪(不会继续构建计算图),因为如果我们没有这个上下文管理器,直接在循环里进行params -=learning_rate * params.grad的话,我们实际上是对叶子节点params 进行了原地操作(注意是-=),这是不允许的,因为这会导致a leaf Variable that requires grad is being used in an in-place operation,也就是我们不能修改叶子节点的值,不然会导致其中的梯度grad信息与节点的值不再有计算上的对应关系。
2.如果我们不采用-=的原地更新方式,而采用=-的方式,即params=params - learning_rate * params.grad(本质上是新建了一个内存块params )的话:
def training_loop(n_epochs, learning_rate, params, t_u, t_c):
for epoch in range(1, n_epochs + 1):
# 在backward()前即可
if params.grad is not None:
params.grad.zero_()
t_p = model(t_u, *params)
loss = loss_fn(t_p, t_c)
loss.backward()
print(params.is_leaf) # True, False
params = params - learning_rate * params.grad # -> unsupported operand type(s) for *: 'float' and 'NoneType'
# with torch.no_grad():
# params=params - learning_rate * params.grad
# params.requires_grad=True
if epoch % 500 == 0:
print('Epoch %d, Loss %f' % (epoch, float(loss)))
return params
training_loop(n_epochs = 5000, learning_rate = 1e-2, params = torch.tensor([1.0, 0.0], requires_grad = True), t_u = 0.1 * t_u, t_c = t_c)有报错:unsupported operand type(s) for *: 'float' and 'NoneType',即在第1次循环结束后新的params记录了旧的params 与learning_rate * params.grad的SubBackward(grad_fn),因此新的params.is_leaf的值为False,不再是叶子节点,不具有grad属性了,因而在第2次循环中,params的grad属性就变为None。
3.那如果,我们在with上下文管理器中,用=-呢?
def training_loop(n_epochs, learning_rate, params, t_u, t_c):
for epoch in range(1, n_epochs + 1):
# 在backward()前即可
if params.grad is not None:
params.grad.zero_()
t_p = model(t_u, *params)
loss = loss_fn(t_p, t_c)
loss.backward()
with torch.no_grad():
print(params.requires_grad) # True
params = params - learning_rate * params.grad
print(params.requires_grad) # False -> element 0 of tensors does not require grad and does not have a grad_fn
# params.requires_grad=True
if epoch % 500 == 0:
print('Epoch %d, Loss %f' % (epoch, float(loss)))
return params
training_loop(n_epochs = 5000, learning_rate = 1e-2, params = torch.tensor([1.0, 0.0], requires_grad = True), t_u = 0.1 * t_u, t_c = t_c)仍然报错,这时候我们发现是因为在第1次循环中,新的params 的requires_grad属性变为False了,这是因为torch.no_grad()使得旧的params的requires_grad属性为False,因此即使做了sub的操作,新的params 的requires_grad属性仍然为False,导致第2次循环,无法正常进行梯度计算并传入。解决办法就是在上下文管理器后加一句params.requires_grad=True,重新让这个新params接受梯度计算。但是这样的写法明显没有一开始的-=写法好,即在with管理器中暂时屏蔽自动求导对params的追踪,在不改变其grad和grad_fn属性的情况下,对params的值直接进行修改,可以理解一下下面这个例子:
a = torch.zeros(3,4,requires_grad=True)
b = (a + a).mean()
b.backward()
print(a.grad)
with torch.no_grad():
a += 1
print(a)
print(a.grad)
'''
tensor([[0.1667, 0.1667, 0.1667, 0.1667],
[0.1667, 0.1667, 0.1667, 0.1667],
[0.1667, 0.1667, 0.1667, 0.1667]])
tensor([[1., 1., 1., 1.],
[1., 1., 1., 1.],
[1., 1., 1., 1.]], requires_grad=True)
tensor([[0.1667, 0.1667, 0.1667, 0.1667],
[0.1667, 0.1667, 0.1667, 0.1667],
[0.1667, 0.1667, 0.1667, 0.1667]])
'''实现了在保留a.grad信息的同时,改变了a的值。
扯得有点远了,下面我们回到一开始的代码,还有一个地方是值得说明的:我们都知道PyTorch是动态图机制,具体点说前向传播时构建计算图,反向传播时销毁计算图,再具体一点就是调用backward()时销毁计算图,只留下params叶节点。即每个epoch循环计算图都被构建销毁,只有params的grad值在不断变换,params的值不断根据梯度进行梯度下降的更新。另外,torch.no_grad()一般都被封装到了下面所述的优化器中了。
在上面的代码中,我们其实使用的是批量梯度下降算法(Batch Gradient Descent)进行的参数优化,关于各种梯度下降算法的介绍可以参见这一篇:机器学习--批量梯度下降法、随机梯度下降法、小批量梯度下降法 - Learner- - 博客园,批量梯度下降法是梯度下降的最原始的形式,它是指在每一次迭代时使用所有样本来进行梯度的更新。具体原理不在此赘述。
在实际应用过程中,我们不可能手动更新每个参数,这是非常繁琐的工作,而是借助自动化的优化算法,这些算法被集成到了optim模块中:
import torch.optim as optim
dir(optim)
'''
['ASGD',
'Adadelta',
'Adagrad',
'Adam',
'AdamW',
'Adamax',
'LBFGS',
'NAdam',
...
'_multi_tensor',
'lr_scheduler',
'swa_utils']
'''每个优化器构造函数都接受一个参数列表(张量,通常requires_grad=True)作为第1个输入,传递给优化器的所有参数都保留在优化器对象中,这样优化器就可以更新它们的值并访问它们的grad属性,图解:

每个优化器都有2个公开可访问的方法:zero_grad()和step.zero_grad(),作用是在构造函数中将传递给优化器的所有参数的grad属性归零。而step()将根据不同优化器的不同优化策略对参数进行更新。
现在创建一个SGD优化器,即随机梯度下降法,其具体原理仍然可以参见上文的链接,简单的来说就是不再像BGD那样整个样本集合之后进行参数更新,而是对每一个随机选取的单个样本训练之后都进行一次参数更新:
params = torch.tensor([1.0, 0.0], requires_grad=True)
learning_rate = 1e-5
optimizer = optim.SGD([params], lr=learning_rate, momentum=0.2)下面就把这个optimizer塞到训练的循环里:
def training_loop(n_epochs, optimizer, params, t_u, t_c):
for epoch in range(1, n_epochs + 1):
t_p = model(t_u, *params)
loss = loss_fn(t_p, t_c)
# 不能累加梯度
optimizer.zero_grad()
# 反向传播
loss.backward()
# 利用优化器更新参数
optimizer.step()
if epoch % 500 == 0:
print('Epoch %d, Loss %f' % (epoch, float(loss)))
return params
params = torch.tensor([1.0, 0.0], requires_grad=True)
learning_rate = 1e-2
optimizer = optim.SGD([params], lr=learning_rate, momentum=0.2)
training_loop(n_epochs = 5000, optimizer = optimizer, params = params, t_u = 0.1 * t_u, t_c = t_c)
'''
Epoch 500, Loss 6.153272
Epoch 1000, Loss 3.312179
Epoch 1500, Loss 2.973489
Epoch 2000, Loss 2.933111
Epoch 2500, Loss 2.928297
Epoch 3000, Loss 2.927725
Epoch 3500, Loss 2.927655
Epoch 4000, Loss 2.927649
Epoch 4500, Loss 2.927647
Epoch 5000, Loss 2.927646
'''当然我们可以用更智能的Adam优化器,稍微有点复杂,但其学习率是自适应的,而且对变量的缩放并不是很敏感,只需简单的将优化器设置为optimizer=optim.Adam([params], lr=learning_rate)。
之后,本章简单的利用索引的方式划分训练集、验证集和测试集,并且介绍了过拟合、欠拟合的概念,以及补充了对torch.no_grad()的说明:在上文中已经叙述过,我们可以把计算模型验证集误差的代码部分都放到with torch.no_grad()里,进而避免了因为要计算验证集误差需要构建的计算图带来的内存开销,这在大参数量的模型上是比较重要的:
def training_loop(n_epochs, optimizer, params, train_t_u, val_t_u, train_t_c, val_t_c):
for epoch in range(1, n_epochs + 1):
train_t_p = model(train_t_u, *params)
train_loss = loss_fn(train_t_p, train_t_c)
with torch.no_grad():
val_t_p = model(val_t_u, *params)
val_loss = loss_fn(val_t_p, val_t_c)
assert val_loss.requires_grad == False
optimizer.zero_grad()
train_loss.backward()
optimizer.step()
if epoch % 500 == 0:
print('Epoch %d, Training Loss %f, Validation Loss' % (epoch, float(train_loss), float(val_loss)))
return params本章小结如下,摘自Page.122:
- 线性模型是用于拟合数据的最简单、最合理的模型;
- 凸优化技术可以用于线性模型,但不能推广到神经网络,所以我们使用随机梯度下降来进行参数估计;
- 深度学习可以用于更一般的模型,这些模型不是为了解决特定的任务而设计的,而是可以自动调整,使自己专注于手头的问题;
- 学习算法相当于根据预测值优化模型参数。损失函数是执行任务时对误差的度量,例如预测输出值和测量值之间的误差,其目标是使损失函数的值尽可能的低;
- 损失函数相对模型参数的变化量可以用来在减小损失的方向上更新相同的参数;
- PyTorch中的optim模块,提供了一组随时可用的优化器,用于更新参数和最小化损失函数的值;
- 优化器使用PyTorch的自动求导特征来计算每个参数的梯度,这取决于该参数对最终输出的贡献,这允许用户在复杂的正向传播过程中依赖动态计算图;
- 像torch.no_grad()这样的上下文管理器,可以用来控制自动求导的行为;
- 数据通常被分为训练样本和验证样本两组,这让我们可以根据没有受过训练的参数来评估模型;
- 当模型在训练集上的性能持续提高而在验证集上的性能下降时,就会发生过拟合,这通常是由于模型没有进行泛化,而只记住了训练集的期望输出。


