如何理解最优化搜索中的Wolfe准则？

日期：2024-08-12 02:10 | 人气：

i) $f(\\mathbf{x}_{k}+\\alpha _{k}\\mathbf{p}_{k})\\leq f(\\mathbf{x}_{k})+c_{1}\\alpha _{k}\\mathbf{p}_{k}^{\\mathrm{T}}\ abla f(\\mathbf{x}_{k})$

ii) $-\\mathbf{p}_{k}^{\\mathrm{T}}\ abla f(\\mathbf{x}_{k}+\\alpha _{k}\\mathbf{p}_{k})\\leq -c_{2}\\mathbf{p}_{k}^{\\mathrm{T}}\ abla f(\\mathbf{x}_{k})$

with $0<c_{1}<c_{2}<1$ .

讲讲Wolfe准则是怎么设计出来的，就很容易理解了。Wolfe 准则主要用于线搜索line search，由两个条件组成，i) Armijo condition和ii) curvature condition。

Armijo condition是充分下降条件，也是最早的提出来了。对于一个基于线搜索的算法，这个条件保证目标函数值序列 $f(\\mathbf{x}_{k})$ 单调下降，如果目标函数有界，那么序列收敛，然而，只用这个条件，无法保证迭代点序列 $\\mathbf{x}_{k}$ 收敛以及局部最优条件。因为对于充分小的步长，Armijo condition都是满足的。给定下降方向产生规则，构造这样一个概念算法: 对每次迭次的下降方向都走小步长 $\\alpha _{k}$ ，并使步长序列 $\\alpha _{k}$ 快速趋于0。这就导致算法快速终止，目标函数值序列虽然收敛，但是没有任何局部最优保证。

从这个概念算法可以推断，只要大步长对于Armijo condition是可以接受的，那么当前迭代点就必然不是局部最优点。所以需要一个条件来得到大步长算法，保证迭代点序列也是收敛的。curvature condition的作用就是拒绝掉满足Armijo condition的那些小步长的，当然还有种说法是使斜率也充分下降。一个疑问就是，充分下降和大步长这两个要求不会冲突吗？Wolfe的贡献是，他证明对于一大类函数和 $0<c_{1}<c_{2}<1$ ，两个条件可以同时满足，也就是Wolfe步长必然存在。

由于保证迭代点序列收敛的关键是大步长。在算法实现时，Wolfe线搜索挺麻烦，所以经常采用Backtracking Armijo line search来避免小步长问题。

最优化方法：无约束（1）牛顿法最优化方法：无约束（2）拟牛顿法最优化方法：无约束（3）信赖域法

Wolfe条件是优化算法中的一种条件，常用于线性搜索以确定步长。它是由两部分组成的，一是足够下降条件（也称为Armijo条件），二是曲率条件。

足够下降条件（Armijo条件）：这个条件确保了新的迭代点能够得到足够的函数值下降。形式化地表述就是，对于某个步长 $c_1 （0 < c_1 < 1）$ ，有以下的不等式： $f(x + αp) ≤ f(x) + c_1 * α * \ abla f(x)^T * p$ 。
曲率条件：这个条件确保了步长不会过大。形式化地表述就是，对于某个步长 $c_2 (c_1 < c_2 < 1)$ ，有以下的不等式： $\ abla f(x + αp)^T * p ≥ c_2 * \ abla f(x)^T * p$ .

其中， $x$ 是当前的迭代点， $p$ 是搜索方向， $α$ 是步长， $\ abla f(x)$ 是在点 $x$ 处的梯度。

Wolfe 条件是用来保证步长选择的有效性，满足这两个条件可以使得函数值有足够的下降，同时步长不会过大。

Armijo条件和Wolfe条件都是在优化算法中选择步长的规则，但：

Armijo条件（也被称为足够下降条件）：主要保证函数值有足够的下降，即新的迭代点的函数值比原来的点降低足够多。这个条件比较宽松，只要满足一定程度的下降就可以，但这可能导致步长过小，搜索过程过于保守。
Wolfe条件：除了需要满足足够的函数值下降（Armijo条件）之外，还需要满足曲率条件，即新的迭代点的斜率不小于原点斜率的某个比例。曲率条件的引入可以避免步长选择过小，保证搜索过程的效率。

在选择 Wolfe 条件中的参数 $c_1$ 和 $c_2$ 时，常见的取值是 $c_1=0.01$ 和 $c_2=0.9$ ，这是经验上的选择。理论上来说， $c_1$ 和 $c_2$ 的选择取决于问题的具体情况和算法的具体需求。唯一的限制是它们必须满足 $0 < c_1 < c_2 < 1$ 。

$c_1$ 的值决定了“足够下降”的程度。较小的 $c_1$ 值意味着只要函数值有一点下降就接受，可能导致步长过大；而较大的值则要求函数值大幅度下降，可能导致步长过小。

$c_2$ 的值影响了曲率条件。较小的 $c_2$ 值可能导致步长过小，使得算法收敛过慢；较大的 $c_2$ 值可能使得步长过大，导致迭代点跳过最优点。

在实践中， $c_1$ 和 $c_2$ 的选择需要根据问题特点和算法性能来调整。 $c_1$ 和 $c_2$ 的取值组合可能会有所不同，具体取决于问题的具体情况和算法的特性。以下是一些常见的组合：

在一般的非线性优化问题中，一般取 $c_1=0.01$ 和 $c_2=0.9$ ，这可以平衡搜索步长的大小和搜索速度。
在一些具有强凸性的问题中，可能会选择 $c_1=c_2=0.5$ ，这样可以确保在每一步都获得一定程度的函数值下降。
在利用牛顿法或者拟牛顿法求解优化问题时，通常取 $c_1=0.01$ 和 $c_2=0.5$ ，这是因为这样的取值可以保证 Hessian 矩阵的正定性，从而保证算法的稳定性。

实际的 $c_1$ 和 $c_2$ 的选择应根据问题的具体情况和算法的具体需求来确定。

以下是一个基于Armijo条件的简单梯度下降优化的 Python 代码例子。

def f(x):
    return x*x*x*x-2*x*x+1

def grad_f(x):
    return 4*x*x*x-4*x

def armijo(x, alpha, p, c1=0.5):
    while f(x + alpha*p) > f(x) + c1 * alpha * grad_f(x) * p:
        alpha *= c1
    return alpha

x = 1.5  # 初始值
alpha = 0.5  # 初始步长
c1 = 0.5  # 足够下降参数
max_iters = 100  # 最大迭代次数

for i in range(max_iters):
    p = -grad_f(x)  # 计算梯度方向
    alpha = armijo(x, alpha, p, c1)  # Armijo条件确定步长
    x = x + alpha*p  # 迭代更新
    print("迭代次数： ", i+1, ": x=", x, ", 步长alpha=", alpha)

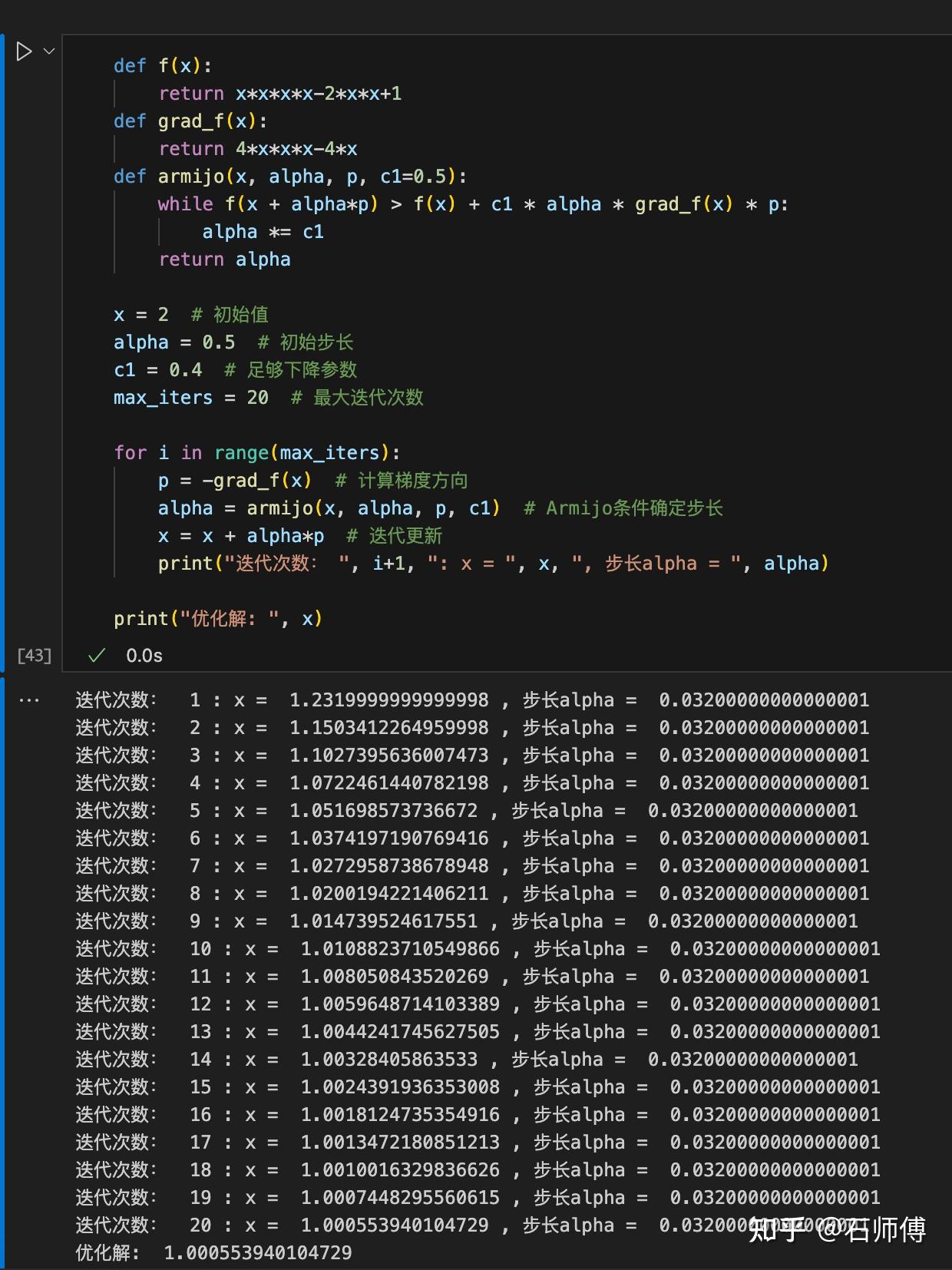
print("优化解: ", x)

以上代码首先定义了目标函数 f(x) 和它的梯度 grad_f(x)。然后，定义了一个实现Armijo条件的函数 armijo()，它通过循环逐渐减小步长 alpha，直到满足Armijo条件。

在优化循环中，首先计算当前位置的负梯度方向 p，然后调用 armijo() 函数确定步长 alpha，最后更新位置 x。

这个例子非常简化，没有处理可能的数值问题，也没有设置收敛条件。整个计算过程收敛速度也很慢，此外，可能需要增加更多函数本身形式的考虑，例如设置更复杂的终止条件，处理可能的数值稳定性等问题。

为了使优化过程更稳定，可以加入终止条件，比如梯度的模小于某个阈值或者函数值的变化绝对值小于某个阈值。以下是添加了终止条件的代码：

tol = 1e-5  # 收敛条件

for i in range(max_iters):

    # 循环的其他部分

    # 检查收敛条件
    if abs(f(x_new) - f(x)) < tol:
        print("优化经过第 ", i+1, " 代已经收敛.")
        break

    x = x_new
    print("迭代次数： ", i+1, ": x=", x, ", 步长alpha=", alpha)

print("优化解: ", x)

tol 作为收敛条件，如果连续两次迭代的函数值变化小于这个阈值，就认为优化已经收敛，然后退出循环。这样可以避免在接近最优解时的无效迭代，提高算法效率。

在实际应用中，优化算法可能会遇到各种数值问题，比如除零错误、数值溢出等。这通常需要根据具体的问题和算法来进行处理。

以下是针对Armijo条件进行了处理可能的数值问题的代码：

def armijo(x, alpha, p, c1=0.5, max_iter=100):
    iter_count = 0
    while f(x + alpha*p) > f(x) + c1 * alpha * grad_f(x) * p:
        alpha *= c1
        iter_count += 1
        # 限制迭代次数以防止无限循环
        if iter_count >= max_iter:
            raise ValueError("Armijo 条件收敛失败！ ")
    return alpha

for i in range(max_iters):
    p = -grad_f(x)  # 计算梯度方向

    # 处理梯度过小的情况
    if np.abs(p) < tol:
        print("梯度过小，已停止迭代")
        break

    try:
        alpha = armijo(x, alpha, p, c1)  # Armijo条件确定步长
    except ValueError as e:
        print(str(e))
        break

    x_new = x + alpha*p  # 迭代更新

进一步地，添加了以下几个处理数值问题的措施：

在Armijo条件的循环中，限制最大的迭代次数，如果超过这个次数还没有找到满足条件的步长，就以错误提示的形式输出。
在优化的主循环中，检查了梯度大小，如果梯度过小（接近零），就停止迭代。因为在这种情况下，已经非常接近最优解，再继续迭代可能会引发数值问题。
使用了 try-except 结构来捕获可能出现的错误。如果在调用 Armijo 条件时出现错误，将打印错误信息并停止迭代。

import numpy as np

def f(x):
    return x*x*x*x-2*x*x+1

def grad_f(x):
    return 4*x*x*x-4*x

def wolfe(x, alpha, p, c1=0.01, c2=0.9, max_iter=100):
    iter_count = 0
    while True:
        lhs = f(x + alpha*p)
        rhs = f(x) + c1 * alpha * grad_f(x) * p
        if lhs > rhs:
            alpha *= c1  # 调整步长
        elif grad_f(x + alpha*p) * p < c2 * grad_f(x) * p:
            alpha *= c2  # 调整步长
        else:
            break
        iter_count += 1
        # 限制迭代次数以防止无限循环
        if iter_count >= max_iter:
            raise ValueError("Wolfe rule failed to converge")
    return alpha

x = 1.4  # 初始值
alpha = 0.5  # 初始步长
max_iters = 100  # 最大迭代次数
tol = 1e-5  # 收敛条件

for i in range(max_iters):
    p = -grad_f(x)  # 计算梯度方向

    # 处理梯度过小的情况
    if np.abs(p) < tol:
        print("The gradient is too small. Stop iterating.")
        break

    try:
        alpha = wolfe(x, alpha, p)  # Wolfe条件确定步长
    except ValueError as e:
        print(str(e))
        break

    x_new = x + alpha*p  # 迭代更新

    # 检查收敛条件
    if abs(f(x_new) - f(x)) < tol:
        print("优化经过第 ", i+1, " 代已经收敛.")
        break

    x = x_new
    print("迭代次数： ", i+1, ": x=", x, ", 步长alpha=", alpha)

print("优化解: ", x)

在这个代码中，定义了一个函数 wolfe() 来执行Wolfe条件的检查。首先检查函数值是否有足够的下降，如果没有，就缩小步长；然后检查曲率条件，如果没有满足，就进一步缩小步长。只有当两个条件都满足时，才接受当前的步长。

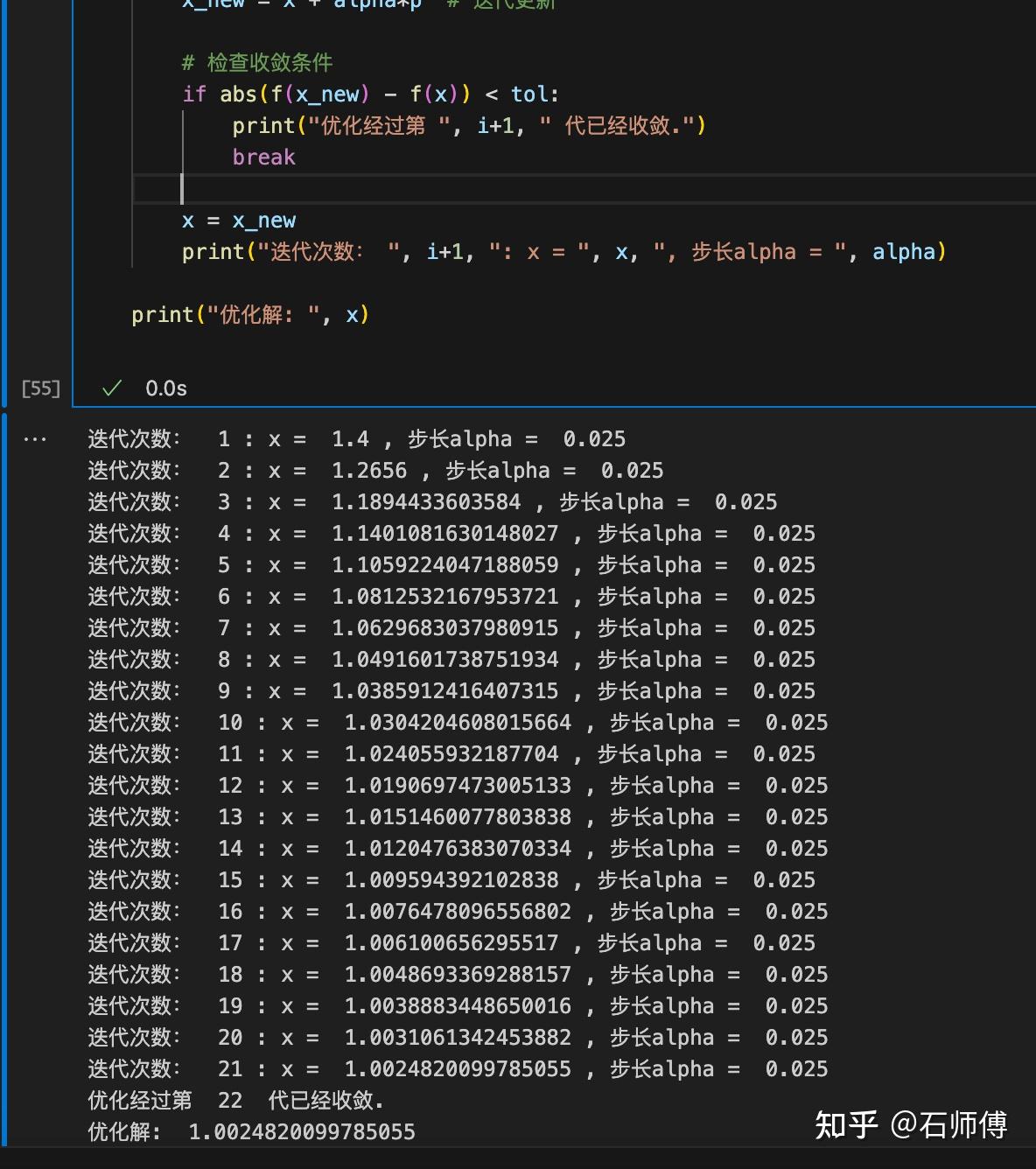
在牛顿法中，利用目标函数的二阶导数信息（也就是Hessian矩阵）来更新迭代点。由于这个例子里面的一阶导数和二阶导数非常简单。以下是利用牛顿法进行优化，并采用Wolfe条件进行线搜索的Python代码：

import numpy as np

def f(x):
    return x*x*x*x-2*x*x+1

def grad_f(x):
    return 4*x*x*x-4*x

def hessian_f(x):
    return 12*x*x-4

def wolfe(x, alpha, p, c1=0.01, c2=0.9, max_iter=100):
    iter_count = 0
    while True:
        lhs = f(x + alpha*p)
        rhs = f(x) + c1 * alpha * grad_f(x) * p
        if lhs > rhs:
            alpha *= c1  # 调整步长
        elif grad_f(x + alpha*p) * p < c2 * grad_f(x) * p:
            alpha *= c2  # 调整步长
        else:
            break
        iter_count += 1
        # 限制迭代次数以防止无限循环
        if iter_count >= max_iter:
            raise ValueError("Wolfe rule failed to converge")
    return alpha

x = 1.5  # 初始值
alpha = 0.5  # 初始步长
max_iters = 100  # 最大迭代次数
tol = 1e-5  # 收敛条件

for i in range(max_iters):
    p = -grad_f(x) / hessian_f(x)  # 牛顿法更新方向

    # 处理梯度过小的情况
    if np.abs(p) < tol:
        print("The gradient is too small. Stop iterating.")
        break

    try:
        alpha = wolfe(x, alpha, p)  # Wolfe条件确定步长
    except ValueError as e:
        print(str(e))
        break

    x_new = x + alpha*p  # 迭代更新

    # 检查收敛条件
    if abs(f(x_new) - f(x)) < tol:
        print("优化经过第 ", i+1, " 代已经收敛.")
        break

    x = x_new
    print("迭代次数： ", i+1, ": x=", x, ", 步长alpha=", alpha)

print("优化解: ", x)

这段代码中，新增了一个函数 hessian_f(x) 来计算目标函数的二阶导数。在牛顿法的更新方向 p 的计算中，用梯度除以二阶导数。其他部分与前面的代码类似。

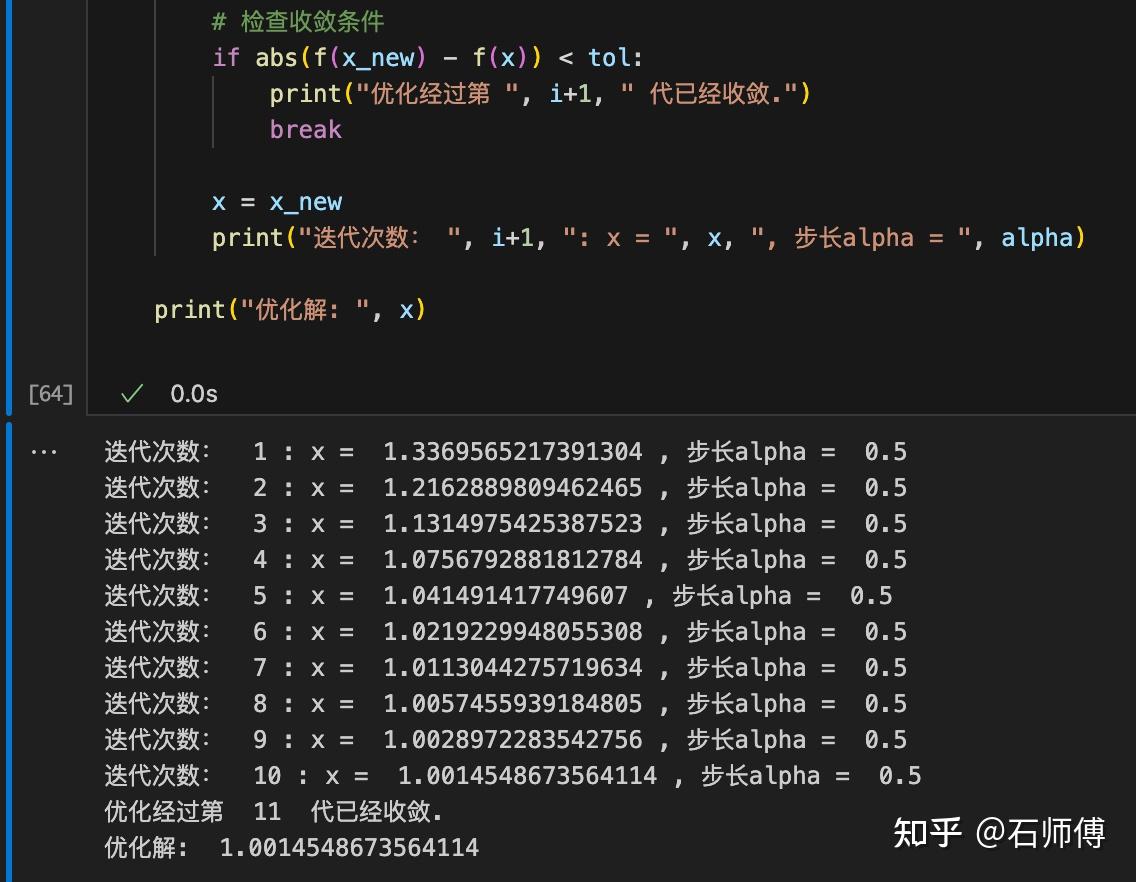
进一步，对与测试函数Rosenbrock函数，初值选择和步长调整重要。需要适当调整初始值和步长选择策略以改进收敛性。而且BFGS方法中Hessian矩阵的更新也十分重要。需要确保更新策略能够适应Rosenbrock函数的特性。

代码如下：

import numpy as np

def rosen(x):
    return 100.0*(x[1]-x[0]**2.0)**2.0 + (1-x[0])**2.0

def grad_rosen(x):
    return np.array([-400*x[0]*(x[1]-x[0]**2) - 2*(1-x[0]), 200*(x[1]-x[0]**2)])

def wolfe(x, alpha, p, c1=0.01, c2=0.9, max_iter=100):
    iter_count = 0
    while True:
        lhs = rosen(x + alpha*p)
        rhs = rosen(x) + c1 * alpha * np.dot(grad_rosen(x), p)
        if lhs > rhs:
            alpha *= 0.5
        elif np.dot(grad_rosen(x + alpha*p), p) < c2 * np.dot(grad_rosen(x), p):
            alpha *= 2
        else:
            break
        iter_count += 1
        if iter_count >= max_iter:
            raise ValueError("Wolfe rule failed to converge")
    return alpha

x = np.array([-1.2, 1.0])  # 初始值
alpha = 1.0  # 初始步长
H = np.eye(2)  # 初始化Hessian矩阵的逆矩阵
max_iters = 10000  # 最大迭代次数
tol = 1e-6  # 收敛条件

for i in range(max_iters):
    g = grad_rosen(x)
    p = -H @ g  # BFGS更新方向

    if np.linalg.norm(g) < tol:
        print("The gradient is too small. Stop iterating.")
        break

    try:
        alpha = wolfe(x, alpha, p)
    except ValueError as e:
        print(str(e))
        break

    x_new = x + alpha*p
    g_new = grad_rosen(x_new)

    # 更新Hessian矩阵的逆矩阵
    s = x_new - x
    y = g_new - g
    rho = 1.0 / np.dot(y, s)
    H = (np.eye(2) - rho * np.outer(s, y)) @ H @ (np.eye(2) - rho * np.outer(y, s)) + rho * np.outer(s, s)

    if np.abs(rosen(x_new) - rosen(x)) < tol:
        print("优化经过第 ", i+1, " 代已经收敛.")
        break

    x = x_new
    print("迭代次数： ", i+1, ": x=", x, ", 步长alpha=", alpha)

print("优化解: ", x)

此处： 1. 将初始步长alpha设置为1.0。这是因为对于Rosenbrock函数来说，较大的初始步长可能有助于算法跳出初始区域。 2. 在Wolfe条件中，步长调整策略改为乘以0.5（如果lhs > rhs）或乘以2（如果lhs <=rhs）。 3. 最大迭代次数max_iters适当增大，以保证算法有足够的时间来收敛。 4. 将收敛条件tol设置尽量小，使得算法在优化解足够接近真解时停止迭代。

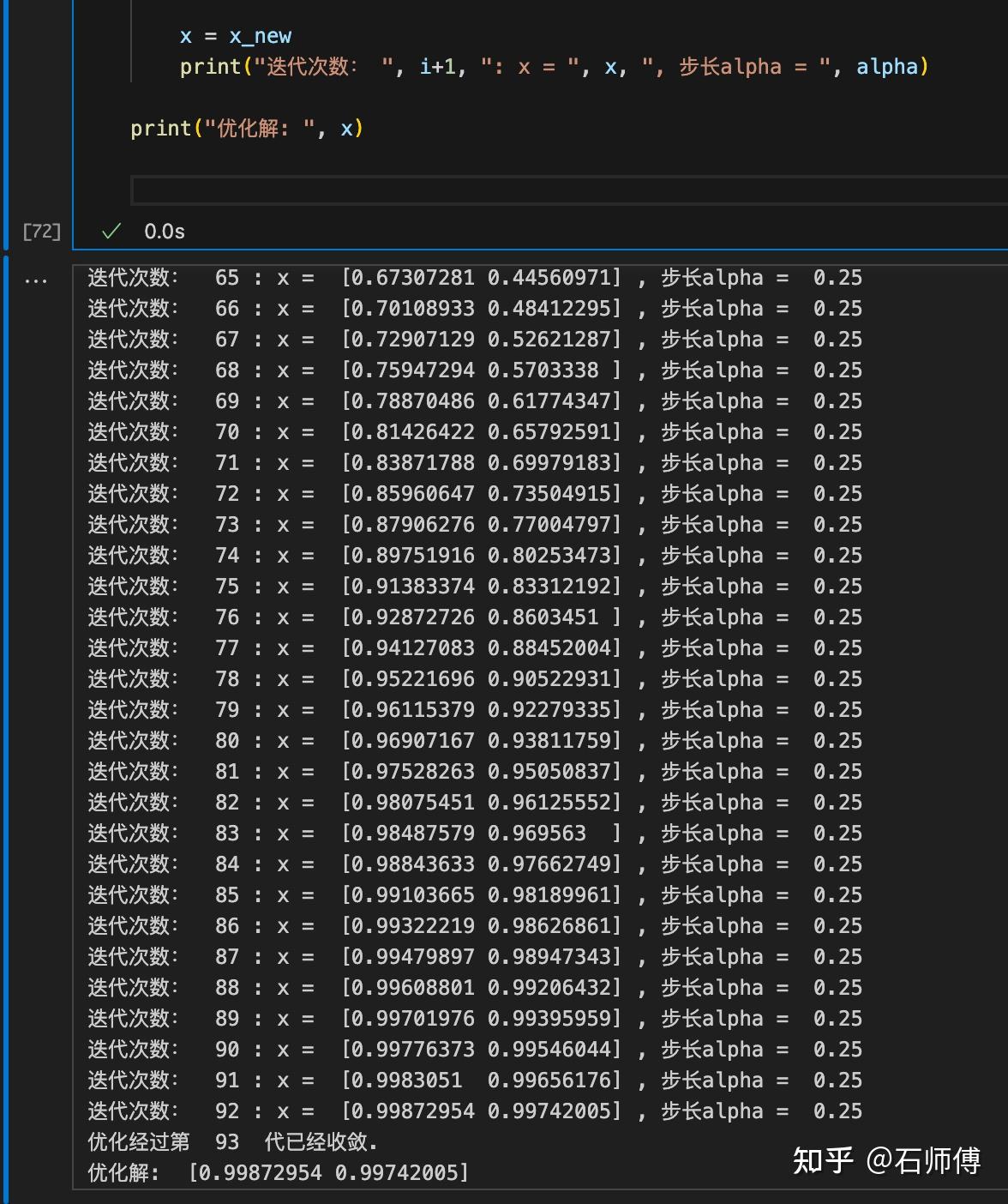
在优化算法中，其他优化算法如BFGS方法可用于确定迭代的方向，而Wolfe条件主要用于确定迭代的步长。可以结合在一起使用，构成了完整的优化算法。

在不考虑步长策略的情况下，如果直接使用拟牛顿法，那么在每次迭代时可能会选择一个默认的步长，比如设为1。然而，这样的步长可能并不总是最优的。在一些情况下，如果步长过大，那么算法可能会跳过最优解；反之，如果步长过小，那么算法可能会需要更多的迭代次数才能收敛到最优解。

相比之下，Wolfe条件提供更为智能的步长选择方法。Wolfe条件考虑了目标函数值和梯度的信息，以确保所选步长能够在保证足够的下降量的同时，也不会导致梯度下降过快。这使得优化算法在很多情况下能够更快地收敛到最优解。

总的来说，其他梯度方法和Wolfe条件的结合，使得算法能够在每一步迭代中，同时考虑到最优的迭代方向和最优的步长，从而提高了优化算法的效率和精度。

可以看看我的视频

【最优化基础---非精确一维搜索：Armijo、Goldstein、Wolfe和强Wolfe条件；回溯法、内插公式和外插公式-哔哩哔哩】 https://b23.tv/hYSQuFd

天辰娱乐-注册登录站400-999-8899
回转火锅设备定制专家

如何理解最优化搜索中的Wolfe准则？

天辰资讯

快速联系

旋转小火锅定制流程

免费咨询

提供图纸

免费设计

免费报价

无忧安装

终身维护