新的优化器 Adan
日期:2024-06-24 13:28 | 人气:
论文题目:Adan: Adaptive Nesterov Momentum Algorithm for
Faster Optimizing Deep Models
作者单位:Sea AI Lab,北京大学,南开大学
论文代码:https://github.com/sail-sg/Adan
自适应梯度算法借用重球加速度的移动平均思想来精确估计梯度的一阶和二阶矩以加速收敛。然而,已有文献表明,Nestrov加速度比重球加速度快,在实验例子中,Nestrov方法在自适应梯度设置下的研究相对少。在这项工作中,我们提出了一种动量算法 Adan,以有效地加速深度神经网络的训练。Adan首先使用一个普通的Nestrov加速度来求出一种新的 Nesterov momentum estimation(NME)方法,这样做避免了在推断时计算梯度的额外计算和内存开销。Adan引导NME在收敛加速的自适应梯度算法中估计梯度的一阶和二阶矩。除此之外,我们证明Adan在非凸随机问题(如深度学习问题)上,在
O
(
n
?
3.5
)
O(n^{-3.5})
O(n?3.5)随机梯度复杂度内找到一个近似值为
n
n
n一阶平稳点来匹配下界。
广泛的研究结果表明Adan在CNN和transformers以及最新的网络和架构上都是Sota的优化器,也对应提高了原有模型的表现。比如:ResNet [7], ConvNext [8], ViT [9], Swin [10], MAE [11], LSTM [12], TransformerXL [13] and BERT [14],这些经典模型都是如此。
更重要的是,Adan能够在使用一半的训练epoch数的情况下达到更好的效果,使得模型能够接受更大的批量的训练,batch size∈1000-32k。这都是之前的优化器做不到的。
深度神经网络(DNNs)在许多领域都取得了显著的成功,如计算机视觉(ResNet、2020s convnet盘点) 和自然语言处理。这种成功的一个显著部分是基于随机梯度的优化器,它们能高效地找到令人满意的解。在目前的深度优化器中,SGD随机梯度下降优化算法是最具有代表性的,它很简单也很直接,对所有梯度坐标采用单一通用学习速率,但是这种方法对稀疏数据或病态问题收敛速度不理想。近年来,人们提出了自适应梯度算法[1-3,22-28],根据损失目标的当前几何曲率,调整每个梯度坐标的学习率。如 Adam、AdamW等都是应用广泛的更快的加速优化器。
然而,并不存在能够战胜一切的完美优化器,都是根据模型的框架和应用的领域来调整的。例如,对于cnn,SGD通常比Adam等自适应梯度算法获得更好的泛化性能,而在视觉变压器(ViTs)[9,10,29]上,SGD经常失败,而AdamW是具有更高性能和更稳定性能的主要优化器。此外,这些常用的优化器在大批量训练中失败,但这是流行分布式训练的默认设置。虽然有一些性能下降,但由于训练时间难以忍受,我们仍然倾向于为大规模深度学习训练任务选择大批量设置。
例如,用512的批量大小训练ViT-B通常需要几天的时间,但当批量大小达到32K时,我们可以在3小时[30]内完成训练。虽然一些方法,如LARS [31]和LAMB [4],已经被提出来处理大的批大小,但它们的性能通常在不同的批大小之间有显著差异。这种性能不一致性增加了培训成本和工程负担,因为人们通常必须为不同的体系结构或培训设置尝试各种优化器。
当我们重新考虑当前的自适应梯度算法时,我们发现它们主要借用重球加速度技术的移动平均思想来估计梯度[1–4]的一阶和二阶矩。然而,[5,32,33]先前的研究表明,Nestrov加速度理论上可以实现比重球加速度更快的收敛速度,因为它在当前解决方案的外推点使用梯度,并看到一个轻微的“未来”。此外,最近的一项工作显示了内斯特夫加速在大批量训练[34]中的潜力。因此,我们被启发考虑有效地集成Nestrov加速度与自适应算法。
本文的贡献:
(1)我们提出了一种有效的Nesterov动量算法(Adan)来训练dnn。Adan开发了一种Nesterov动量估计方法来估计自适应梯度算法中稳定和准确的梯度第一和第二动量。
2)此外,Adan比以往的自适应梯度算法具有更快的收敛速度。
3)经验证明,Adan在cnn和transformers上显示出比SoTA深度优化器更高的泛化性能。
下面是我们的详细贡献。
首先,我们提出了一种有效的Nesterov式加速诱导深度学习优化器,称为Adan。给定一个方法
f
f
f,以及当前的解决方案
θ
k
θ_k
θk?,Nesterov加速度公式估计当前的梯度
g
k
=
?
f
(
θ
k
′
)
g_k=
abla f(θ^{'}_k)
gk?=?f(θk′?),推算点
θ
k
′
=
θ
k
?
η
(
1
?
β
1
)
m
k
?
1
θ^{'}_k = θ_k - \eta (1-\beta_1)m_{k-1}
θk′?=θk??η(1?β1?)mk?1?,其中学习率是
η
\eta
η,
β
1
\beta_1
β1?属于(0,1)。动量更新公式:
m
k
=
(
1
?
β
1
)
m
k
?
1
+
g
k
m_k=(1-\beta_1)m_{k-1}+g_k
mk?=(1?β1?)mk?1?+gk?,然后每个step,按照
θ
k
+
1
=
θ
k
?
η
m
k
θ_{k+1}=θ_k-\eta m_k
θk+1?=θk??ηmk?,可以看出来,在求
θ
k
′
θ^{'}_k
θk′?时,
θ
k
θ_k
θk?也被求出来了。这就导致了参数计算的内存开销,如何解决呢?
我们提出NME方法,首先,计算梯度
g
k
=
?
f
(
θ
k
′
)
g_k=
abla f(θ^{'}_k)
gk?=?f(θk′?)和当前的θ并且估计一个移动梯度平均量,
m
k
=
(
1
?
β
1
)
m
k
?
1
+
g
k
′
m_k=(1-\beta_1)m_{k-1}+g^{'}_k
mk?=(1?β1?)mk?1?+gk′? ,其中,
g
k
′
=
g
k
+
(
1
?
β
1
)
(
g
k
?
g
k
?
1
)
g^{'}_k=g_k+(1-\beta_1)(g_k-g_{k-1})
gk′?=gk?+(1?β1?)(gk??gk?1?)。这样做首先可以看出和普通的Nesterov法是等价的,并且减少了
θ
{
′
}
k
θ{'}_k
θ{′}k?的输出,并且接下来的步骤是,将KaTeX parse error: Expected '}', got 'EOF' at end of input: g^{']_k作为当前的随机梯度,并应用到已有的梯度下降算法中,比如用到Adam中。我们可以估计第一动量,
m
k
=
(
1
?
β
1
)
m
k
?
1
+
β
1
g
k
′
m_k=(1-\beta_1)m_{k-1}+\beta_1 g^{'}_k
mk?=(1?β1?)mk?1?+β1?gk′?和和第二动量,
n
k
=
(
1
?
β
2
)
n
k
?
1
+
β
2
(
g
k
′
)
2
n_k=(1-\beta_2)n_{k-1}+\beta_2 (g^{'}_k)^2
nk?=(1?β2?)nk?1?+β2?(gk′?)2的计算。最后,更新参数,
θ
k
+
1
=
θ
k
+
η
m
k
n
k
+
?
θ_{k+1}=θ_k+\frac{\eta m_k}{\sqrt{n_k+\epsilon}}
θk+1?=θk?+nk?+??ηmk??
相关的工作还有AdaGrad、Adabound、Adabelief、RMSProp、Adam、Padam、NAdam等有兴趣的可以下载。在一篇综述中,有详细介绍前面几个优化器算法的理论和证明。
这篇文章的精髓应当是在公式的具体推导过程中,作为一个凸优化的省空间的解决思路,在证明近似解的过程中应当有许多有意思的说法和理论,值得一看!
实验结果:
首先展现的是关于ResNet和ConvNext在imageNet的训练结果,可以说在整体上有着不错的提高,并且比现有的几种优化方法取得的效果都好。

然后,实验在ViT和Swintransformer上也实现了性能的提升,并且特意把epoch的数目标出来,展现了摘要中所说的仅用一半的epcoch数目就能够使得模型的训练达到一个更优的效果。

这一张图主要是ViTs和ResNet训练的损失记录。



以上均是实验给出的效果展示,其实从公式的推导过程中我们可以发现,Adan确实能够加快模型的训练,实验更是给出了令人信服的结果。
这块儿是个大工程:
我慢慢敲吧!
从AdaGrad和RMSProp开始,自适应梯度算法比SGD有着更快的收敛速度,跟进一步,Adam和AdamW已经成为训练CNN和Vits的首选优化器。自适应算法能够调整目标函数的当前的几何曲率来训练参数,因此收敛得更快。
考虑一个随机梯度估计:
g
k
:
=
E
ζ
?
D
[
?
f
(
θ
k
,
ζ
)
]
+
?
k
g_k:=E_{\zeta ~ D}[
abla f(θ_k, \zeta)] + \epsilon_k
gk?:=Eζ?D?[?f(θk?,ζ)]+?k?
其中
?
k
\epsilon_k
?k?是噪声,
RMSProp和Adam分别是

这里,
m
0
=
0
m_0=0
m0?=0,尺度常数
η
\eta
η是当前的学习率,
。
。
。表示点乘, 在RMSProp的基础上,Adam使用之前的平均梯度m来代替,和经典的HBA 重球加速方法很类似。
HBA:
g
k
=
?
f
(
θ
k
)
+
?
k
g_k=
abla{f(θ_k)} + \epsilon_k
gk?=?f(θk?)+?k?,
m
k
=
(
1
?
β
1
)
m
k
?
1
+
g
k
m_k=(1-\beta_1)m_{k-1}+g_k
mk?=(1?β1?)mk?1?+gk?,
θ
k
+
1
=
θ
k
?
η
m
k
θ_{k+1}=θ_k-\eta{m_k}
θk+1?=θk??ηmk?。
Adam和HBA采用的都是向平均梯度的方向进行转移,尽管HBA更简单。也就是说越大梯度,加速收敛得越快。
对于HBA,还有另一个改进版本,叫AGD,
AGD:
g
k
=
?
f
(
θ
k
?
η
(
1
?
β
1
)
m
k
?
1
)
+
?
k
g_k=
abla{f(θ_k-\eta(1-\beta_1)m_{k-1})}+\epsilon_k
gk?=?f(θk??η(1?β1?)mk?1?)+?k?,
m
k
=
(
1
?
β
1
)
m
k
?
1
+
g
k
m_k=(1-\beta_1)m_{k-1}+g_k
mk?=(1?β1?)mk?1?+gk?,
θ
k
+
1
=
θ
k
?
η
m
k
θ_{k+1}=θ_k-\eta{m_k}
θk+1?=θk??ηmk?。
区别在于,AGD的梯度是
θ
k
′
=
θ
k
?
(
1
?
β
1
)
(
θ
k
?
θ
k
?
1
)
θ^{'}_k=θ_k-(1-\beta_1)(θ_k-θ_{k-1})
θk′?=θk??(1?β1?)(θk??θk?1?)
因此,在模型的训练处于斜率不变时,AGD的收敛会更快,所以在理论上,AGD更适合深度学习模型,在凸优化的问题上能够得到更好的解。
对于大批量训练,最近的工作表明,AGD有潜力实现与一些专门设计的优化器相当的性能,如LARS和LAMB。由于其在收敛性和大批量训练方面的优势,我们考虑应用AGD来改进自适应算法。
Lemma 1.
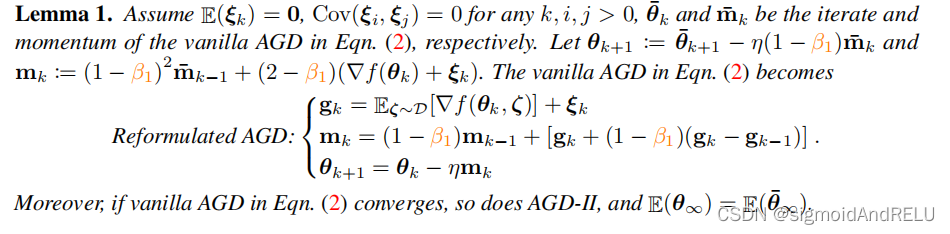
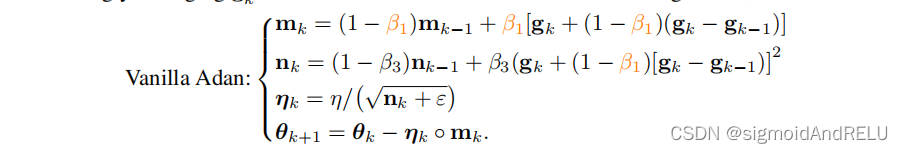

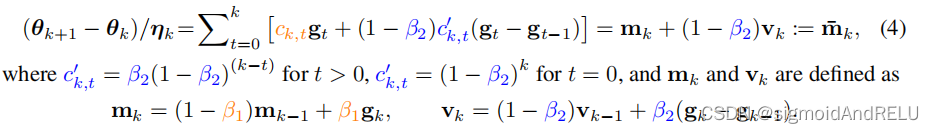

4、收敛分析

上图是对算法中最重要的公式的截图,具体的内容明天再加!
休息一下!


